Shear alignment of fatty acid monolayers

SHEAR ALIGNMENT OF FATTY ACID MONOLAYERS

We have performed experiments consisting on the application of simple shear on a fatty acid monolayer on the air-water interface. Using Docosanoic acid (C₂₂), we have explored the coupling between simple shear flow and the structure of different tilted condensed phases: L₂, L₂' and Ov. Using Brewster Angle Microscopy we have observed that a rich variety of dramatically different effects can be seen, depending on the phase of the monolayer, the surface pressure and the applied shear rate (for an overview and details of the experimental apparatus, please go here).
Experiments start by spreading a monolayers on the air-water interface and, after reaching the desired thermodynamic conditions, a series of shear cycles are applied. The velocity of the flow is inverted in each half of one cycle.

We find two particularly interesting types of behaviors (go here for further details):

A continuous change in the reflectivity in regions of the monolayer, consistent with a flow-induced rotation of the azimuth orientation of the fatty acid tails which suggests the possibility of tumbling of the fatty acid molecules. This behavior is observed both in the L₂ and in the L₂' phases (for low values of the surface pressure and the shear rate). This behavior is not observed in the Ov phase, for any pressure or shear rate.
Discontinuous changes in the reflectivity, which appear in the form of propagating fronts. These fronts can be observed in all three phases: in the L₂ and L₂' phases the surface pressure and the shear rate must be above a certain value for the fronts to appear. In the Ov phase, however, the fronts appear for virtually any combination of pressure and shear rate.

In this brief report we detail the observations in the Ov phase. We have seen that the nature of the changes induced by the application of shear flow on the monolayers are consistent with shear alignment of the fatty acid monolayers, so that the azimuth orientation of all domains maintains a fixed angle with respect to the direction of the flow.

Qualitative observations

When the fatty acid monolayer is first spread on the air-water interface and the conditions of pressure and temperature are set so that it is in the Ov phase, a mosaic with domains of multiple reflectivities can be observed, consistent with the fact that there are no constraints on the value of the azimuth of the fatty acid tails.
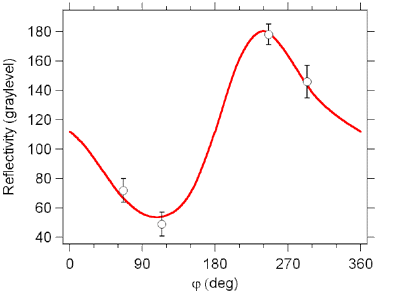
Almost immediately after the shear flow is stablished, a sudden transition takes place: straight fronts propagate across all domains until only two highly contrasted values of the reflectivity are observable (see Figure 1). An analysis of the correspondence between observed reflectivity and tilt azimuth shows that the highest contrast will be between domains that are almost aligned with the flow, with domains with an azimuth of j ~ 90º (to the right of the laser beam) appearing dark, and domains with an azimuth of j ~ -90º (to the left of the laser beam) appearing bright. This suggests that the fatty acid tails may be aligned by the flow.
Inversion of the flow orientation suggests that the domains are not exactly aligned along the flow, but aligned maintaining a fixed angle with the flow direction. Upon inversion of the flow, new fronts appear in all the domains, both in the bright and in the dark domains. In the example shown in Figure 1, both types of domains are slightly darkened by the propagating fronts, but the domains that were darker prior to the inversion of the flow remain also darker afterwards.

Alignment of a monolayer under shear Figure 1. C22 monolayer under shear. T = 47 ºC, p = 21 mN/m (Ov phase), g = 0.2 s^-1. The line segment on frame (a) is 100 mm long. The diagrams on frames (a) and (h) indicate the orientation of the shear flow.
A fresh monolayer undergoes a single shear cycle. Upon formation, domains of many reflectivities are observable in the monolayer. Upon application of shear, domains readjust their reflectivities by formation and propagation of fronts (a-d). Notice that the domain structure in (d) shows an increased contrast between domains, and only two possible reflectivities are observable. Orthogonal fronts (either vertical or horizontal) appear within 0.1s of the application of shear (b). The speed at which fronts propagate is shear-rate-dependent. Time elapsed between (b) and (c) is 0.1s. The flow is stopped after about 5s (d).
When the flow is inverted in the second half of the cycle (e-f), propagation of bands is observable in most domains. Frame (e) is recorded 0.4s since shearing started, and the elapsed times are: from (e-f), 0.13s; from (f-g), 0.1s. Frame (h) is recorded 0.21s since shearing started. Even though individual domains can still be compared, the structure of the monolayer and the distribution of reflectivities are irreversibly changes.
An quicktime file with a live video of this experiment is available here.

As the experiment goes on with a series of shear reversal cycles, these slight changes in domain reflectivity keep taking place. When the flow has one orientation, both dark and bright domains decrease their reflectivity, and when the flow has the opposed orientation, both types of domains increase their reflectivity. It is important to remark that, in these observations, the mosaic of domains remains roughly unaltered. A quicktime file showing two consecutive shear inversions can be found here. Note that, since these images are obtained after a series of shear reversal cycles have been applied, the monolayer is already annealed so that only two reflectivities exist under flow conditions in the steady state.

Analysis and discussion. Shear alignment.

The above observations suggest that shear alignment is the phenomenon responsible for the changes in reflectivity. In Figure 2, the reflectivity as a function of the azimuth has been calculated using physical parameters found in the literature and that can be used for C₂₂ in the Ov phase. The reflectivity depends strongly on the polar tilt. A value q = 20º has been used to compute the reflectivity curve in this example, but we will estimate the value of the polar tilt in the calculations we report below. We make the hypothesis that the two alternate reflectivities we observe in the dark domains under shear correspond to an orientation with an azimuth j = 90º ± a, where a is the alignment angle. Similarly, we make the hypothesis that the two alternate reflectivities observed in the bright domains under shear correspond to an azimuth j = 270º ± a. The two alternate reflectivities are stable either for clockwise shear or for counterclockwise shear (see Figure 3). Note that the flow, perpendicular to the incidence plane, is parallel to the j = 90º and j = 270º directions. It is important to remark that if we stop shearing while the reflectivity transitions are under way (propagation of fronts) the configuration of the monolayer in the absence of shear does not change in time (all reflectivities coexist and are stable). Taking into account that, in the absence of shear, the polar tilt angle is fixed but the azimuth angle is free, we conclude that the changes in reflectivity we observe are indeed due only to changes in the azimuth.



Counter-clockwise shear	Clockwise shear

Figure 2. Reflectivity from a Langmuir monolayer as a function of the azimuth. The grayscale on top corresponds to an 8-bit rendering of the reflectivity curve. The curve has been calculated using the transfer matrix formalism and using physical parameters found in the literature for C₂₂ in the Ov phase. The polar tilt is taken to be q = 20º. The lines mark the reflectivities that dark (blue lines) and bright (red lines) domains will exhibit under shear for an alignment angle a ~25º.

Figure 3. Modelization of the observed reflectivity changes induced by shear. The top two diagrams correspond to the dark domains, and the bottom two diagrams correspond to the bright domains. The direction of the flow is along the horizontal (perpendicular to the laser beam). A change in the orientation of the flow induces a 2a shift in the azimuthal orientation, which is observed as a small change in the reflectivity of both types of domains.

In order to test the above hypotheses, and to prove more convincingly that we are indeed observing shear alignment with a characteristic alignment angle, we want to measure the value of the alignment angle, and study how it changes with the applied surface pressure.
Our procedure consists on matching the four reflectivities that characterize the possible orientation of domains in the monolayer under shear with the shape of the reflectivity curve. The shape of this curve, however, changes significantly with the value of the polar tilt angle. Therefore, it is required that we have a good knowledge of the value of the polar tilt in our Ov monolayers, for each applied surface pressure.
The polar tilt of the fatty acid tails can be related with a simple geometric argument with the area occupied by each molecule in the condensed phase, namely, cos(q) = A₀/A, where A₀is the area per molecule for the untilted phase (the LS phase, which is attained by compressing the Ov phase). By measuring the p-A isotherms, we notice that in the Ov phase it is a good approximation to use a linear relationship, p= a + b A. With this, the polar tilt angle can be related to the surface pressure by cos(q) = (a - p₀)/(a - p). Extracting the parameter a from our data (intercept of the straight line isotherm) we can quite accurately estimate q as a function of p (see Figure 6).

Measurement of the alignment angle.
For a given surface pressure, we obtain the image of a monolayer under shear where the four possible reflectivities are observable. The image is digitized into an 8-bit grayscale and the gray level for each of the four reflectivities is measured (see Figure 4). The four reflectivities are related to four values of the azimuth, according to the above description, namely:

R₁ = R(90-a)
R₂ = R(90+a)
R₃ = R(270-a)
R₄ = R(270+a),

where R(j) is the digitized reflectivity curve.

Our goal is to extract the value for the alignment angle, a, that best fits the four reflectivities to the reflectivity curve expected for the current surface pressure. Since we do not have an absolute callibration for the correspondence between reflectivity and gray level in our images, we will assume that the digitization will fit the full range of reflectivities between the gray levels R_min and R_max.
Therefore, the process of fitting the four reflectivites to the reflectivity curve involves obtaining three fitted parameters, R_min , R_max, and a (see Figure 5).

Figure 4. Four reflectivities extracted from a monolayer under shear upon inversion of the flow.

Figure 5. The four reflectivities are fitted to the reflectivity curve to obtain the alignment angle a ~27º.

We have extracted values for the alignment angle for different surface pressures in monolayers in the Ov phase. The results of the measurements are reported on Figure 6. We observe a significant amount of scatter in our data, which is mostly due to the presence of light intensity gradients and diffraction patterns in our images that add a significant amount of noise to the data. Nevertheless, we observe that our data are consistent with alignment angles between 10º and 35º in the range or surface pressure that we have been able to measure. The alignment process can be qualitatively observed for surface pressures as high as p = 29 mN/m (the Ov-LS phase transition takes place at p ~ 31.5 mN/m). The poor contrast of the images, however, makes a quantitative measurement impossible. The alignment angle seems to increase after the L₂-Ov phase transition (p > 13.8 mN/m) and reach a maximum at about p = 21 mN/m. After that, a seems to start decreasing.
In order to make some predictions as to what should be the expected behavior of a as the pressure increases and the monolayer approaches the phase transition to the untilted phase, we will look for insight in the theories that describe shear-induced alignment in nematic liquid crystals.

Figure 6. Estimated alignment angle as a function of surface pressure for Ov monolayers under shear. The green triangles are the estimated values for the polar tilt, as described in the text.

The Eriksen-Leslie-Parodi theory describes the hydrodynamics on nematic liquid crystal phases, and defines six viscosity coefficients that introduce the contribution of different terms in the stress tensor.
In particular, that theory is helpful to describe the possible behavior of a nematic liquid crystal under simple shear. The nematic molecules can either perform periodic tumblings or can be aligned at a certain angle with respect to the direction of the flow.
This alignment angle can be related to a combination of some of the viscosity coefficients, namely,

tan²(a) = a₃/a₂,

or the equivalent expression,

cos(2a) = -l₁/l₂,

where l₁ = a₃-a₂, and l₂ = a₃+a₂.
On Figure 7 we have computed the two above transformations of the alignment angle that one may relate to the ratio of the viscosity coefficients and that one may use to discuss the expected trend as the polar tilt angle decreases to zero.

Figure 7. Transformations that relate the aglinment angle to the ratio of viscosity coefficients in the Eriksen-Leslie-Parodi theory for nematohydrodynamics.