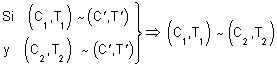Según el principio de homogeneidad respecto a cuantías se cumple que,

Si ....

Si la anterior relación se cumple para , también se cumplirá para :

Si

La última ecuación define implícitamente el cociente de cuantías como función de los diferimientos y :

La función recibe el nombre de factor financiero₄ y es el equivalente de una unidad monetaria de en .

El factor financiero permite calcular la cuantía del capital financiero equivalente al capital en :

El factor financiero cumple las siguientes propiedades que se deducen de la definición de capital financiero y de las propiedades de la equivalencia financiera:

•  El factor financiero es siempre estrictamente positivo:

El factor financiero es, como se ha deducido anteriormente, el cociente entre las cuantías de dos capitales equivalentes y, por tanto, dicho cociente será siempre positivo puesto que, por la propia definición de capital financiero, las cuantías son siempre positivas.

Esta propiedad se basa en el principio de preferencia por la liquidez de la equivalencia financiera.

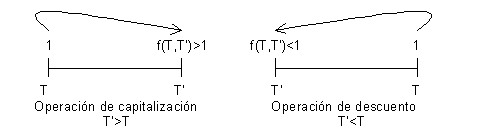
• Si

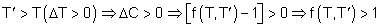
Para (operación de capitalización), el equivalente de una u.m. de en ha de ser mayor a 1.

• Si

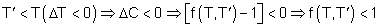
Para (operación de descuento), el equivalente de una u.m. de en ha de ser menor a 1 puesto que se está retrocediendo en el tiempo.

• Si

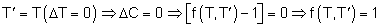
Para , el equivalente de una u.m. de T en T ha de ser igual a 1 puesto que el tiempo no ha transcurrido.

•  El factor financiero y el factor financiero toman valores recíprocos:

Esta propiedad se basa en la propiedad simétrica de la equivalencia financiera.

Dados dos capitales equivalentes ~ se cumple que . Por la propiedad simétrica, también es cierta la equivalencia ~ de la que se deduce que .

Por tanto, se cumplirá que

•  El factor financiero es escindible:

Esta propiedad está basada en la propiedad transitiva de la equivalencia financiera e implica que, desde un punto de vista teórico para hallar la cuantía equivalente de una u.m. de en , da lo mismo hacerlo mediante un único paso que si se divide el plazo en dos.

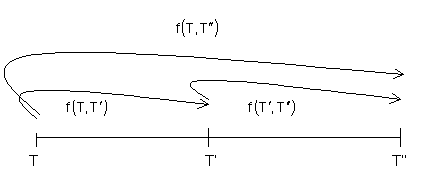
De la equivalencia ~ se deduce que . Igualmente, de la equivalencia ~ se deduce que . Por la propiedad transitiva se cumplirá también que ~ de donde se obtiene que . Este último factor financiero puede expresarse del siguiente modo:

Esta propiedad recibe el nombre también de propiedad circular del factor financiero y se expresa:

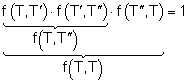
•  El factor financiero es una función creciente respecto a la segunda variable y     decreciente con respecto a la primera variable T.

Si se fija el diferimiento inicial T, la cuantía equivalente de una u.m. de T en será tanto mayor cuanto mayor sea como consecuencia del principio de preferencia por la liquidez y, por tanto, mayor será el factor financiero. Por el contrario si se fija el diferimiento final cuanto más cercano a dicho diferimiento esté el inicial T (cuanto mayor sea T) menor será el factor financiero implicado.

La propiedad transitiva de la equivalencia financiera permite afirmar que

Si además se supone que , por el principio de preferencia por la liquidez se cumplirá que . Por tanto, . Se deduce, por tanto, que cuanto mayor es la segunda variable mayor es el factor financiero.

Igualmente, por la propiedad transitiva de la equivalencia financiera se puede afirmar que

 

Si además se supone que , por el principio de preferencia por la liquidez se cumplirá que . Por tanto, Se deduce, por tanto, que cuanto mayor es la primera variable menor es el factor financiero.

 

En la práctica se utilizan factores financieros que son funciones continuas y con derivadas parciales.
En este caso, se cumplirá que:

 

El factor financiero que cumple todas estas propiedades da lugar a una función exponencial de la forma:

donde es la función precio de la operación de financiación en cada uno de los instantes y recibe el nombre de ley financiera.

Si se supone que (ley financiera estacionaria), entonces la expresión del factor financiero es

Haciendo , se obtiene que

donde A es un parámetro cuyo valor es superior a la unidad.

4 Rodríguez, A. 1994. Matemática de la financiación, pp. 28-38.