Los pactos que caracterizan al régimen financiero de interés compuesto a tanto constante y vencido son:
• El precio o interés total se paga al final de la operación conjuntamente con la devolución de la cuantía inicial.
• El plazo total de la operación se divide en periodos de capitalización y el precio se calcula en cada periodo aplicando una constante de proporcionalidad, i, que es el tanto nominal de interés, a la cuantía acumulada al inicio del periodo considerado y a la extensión del mismo.
Sea:
• 
: Cuantía inicial
• 
: Cuantía acumulada al final del periodo r, 
, siendo 
• 
: Tanto nominal de interés, (tanto anual)
• 
: Plazo de la operación, expresado en años
• 
: Periodo de capitalización, expresado en años
• 
: Frecuencia de capitalización. Es el número de periodos de capitalización en un año. Se cumple que 
• n: Número de periodos de capitalización en que se divide el plazo de la operación. Se cumple que 
El esquema temporal correspondiente a este régimen es:
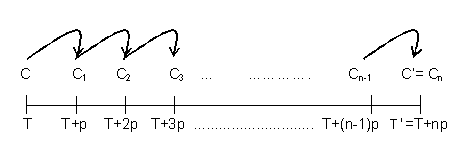
y la evolución de la cuantía periodo a periodo:
La relación entre la cuantía final y la cuantía inicial en el régimen financiero de interés compuesto a tanto constante y vencido es:
o bien,
Esta ecuación cumple todas las propiedades de la equivalencia financiera, lo que implica que el factor financiero empírico que se deduce de este régimen verifica a su vez todas las propiedades del factor financiero teórico, siendo su expresión:
Se trata de una función exponencial cuya representación gráfica es:
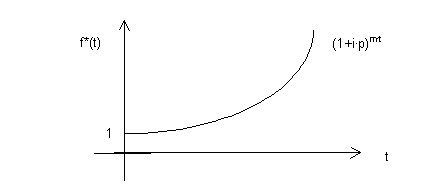
A partir de la expresión que caracteriza al régimen financiero de interés compuesto a tanto constante,
se deduce:
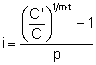
