Una renta fraccionada se caracteriza porque su frecuencia no coincide con la frecuencia de variación del término de dicha renta.
Las características de la renta fraccionada son las siguientes:
• Periodo de la renta: P (Frecuencia de la renta: m=1/P).
• Periodo de la variación del término: P' (Frecuencia de la variación del términ o: M=1/P').
• Número de términos de la renta: n.
• Número de términos de cuantía diferente en el plazo de la renta: N.
• El término general de la renta fraccionada es 
, donde r=1,2,...,N puesto que el término sólo cambia N veces de cuantía.
• Número de términos de igual cuantía dentro de cada periodo de variación: k.
• Se cumple que 
.
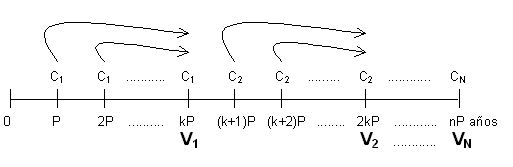
El esquema temporal de una renta fraccionada, vencida, inmediata y temporal , es el siguiente:
Como se desprende del esquema anterior, el término de la renta no varía cada periodo sino que lo hace cada k periodos. Así, durante los k primeros periodos el término es el mismo y se simboliza por C1, durante los k segundos periodos el término también es el mismo y se simboliza por C2, aunque distinto a los primeros k periodos y así sucesivamente. Una renta fraccionada se puede considerar como un conjunto de N rentas constantes.
Para hallar el valor actual de la renta fraccionada se sustituye, en primer lugar, cada una de las N rentas constantes por su valor final:
El valor final de una renta de 
términos de cuantía constante 
y de frecuencia m es:
Así, la renta original puede sustituirse por otra renta de N términos de cuantía variable 
y de periodicidad 
, esto es de frecuencia M, cuyo esquema temporal es:
El valor actual de la renta fraccionada, 
, se obtiene del siguiente modo:
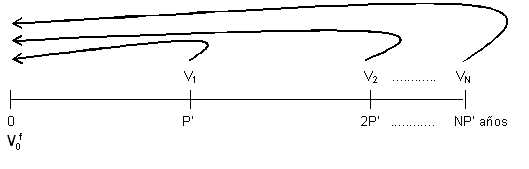
En definitiva,
es el valor actual de una renta, denominada auxiliar, cuyas características son las siguientes:
• Su frecuencia es igual a la frecuencia de variación de la renta fraccionada: M.
• El número de términos (y, por tanto, el número de periodos) coincide con el número de términos de cuantía diferente en todo el plazo de la renta fraccionada: N.
• El término de la renta es 
(r=1,2,...,N) y cada uno de ellos se sitúa donde está el último término de cuantía 
. Así, por ejemplo, el primer término de la renta auxiliar 
se sitúa donde está el último término de cuantía 
.
El esquema de la renta auxiliar asociada al de la renta fraccionada es el siguiente:
La renta auxiliar es una renta variable, vencida, inmediata y temporal y, por tanto, su valor actual se obtiene aplicando las fórmulas de las rentas de variación geométrica o lineal anteriormente vistas en los apartados Renta de variación geométrica y Renta de variación lineal respectivamente.
El cociente 
es el denominado factor corrector, que permite convertir el valor actual de la renta auxiliar en el valor actual de la renta fraccionada, vencida, inmediata y temporal. Dicho factor corrector es el cociente entre el tanto nominal de interés asociado a la frecuencia de la variación y el tanto nominal de interés asociado a la frecuencia de la renta fraccionada.