Physics Accomplishments















Baryon-Baryon Scattering

Since 2004, the NPLQCD collaboration has been calculating the properties and interactions Of A=2,3,4,5 systems. The first comprehensive analysis of light nuclei and hypernuclei at \(m_{\pi}\) ∼ 805 MeV was performed in 2013. Generically, one finds that the nuclei are more deeply bound at heavier pion masses. A latter study was performed in 2017, whose goal was to extend the previous work by the collaboration on the two-nucleon interactions and other two-baryon channels. The merit of such studies at a large value of quark masses is that high precision results are possible, allowing conclusive statements to be made about the physics in play when the input parameters of the Standard Model are varied, and setting the stage for calculations at lower quark masses. In this last study, the scattering amplitudes at low energies are obtained by Lüscher method, allowing to observe directly from QCD for the first time an approximate SU(6) spin-flavor symmetry, consistent with the accidental SU(16) symmetry of nuclear and hypernuclear force in the limit of large \(N_c\).


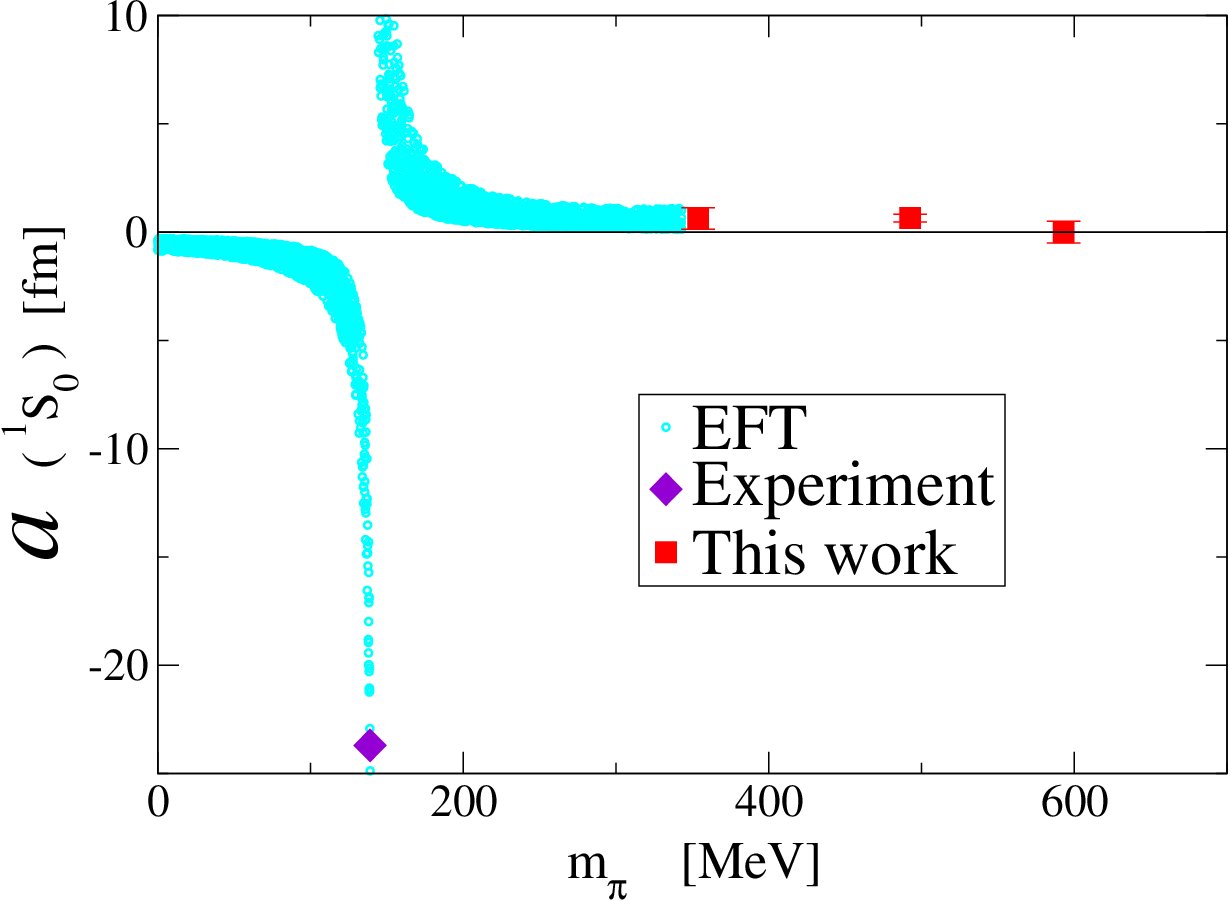
NN 1S0

Nucleon-Nucleon Scattering

In 2005 we performed the first fully-dynamical lattice QCD calculation of the nucleon-nucleon scattering length at pions as light as 350 MeV. The scattering length is found to be of natural size at the pion masses, unlike the unnaturally large scattering lengths found in nature. Only one of the points was at a pion mass within the regime of applicability of the \(\text{NN}\) effective field theories that have been develoiped during the last 15 years, and so we were unable to extrapolate to the physical point. However, in conjunction with the physical point we extrapolated to the chiral limit, finding very curious behaviour. It is possible that in the limit of vanishing quark masses that the scattering lengths in BOTH spin channels diverges, leading to a completely scale-invariant interaction. We have no idea why nature would choose such behaviour, but it is something that must be explored further with lattice QCD calculations at lighter pion masses. In 2013, we continued this study, but using an ensemble at the SU(3) symmetric point with a pion mass of \(m_{\pi}\) ∼ 800 MeV. And for the first time, the effective ranges of the \(\text{NN}\) interactions were determined using lattice QCD. Then, in 2015, we perfomed an exhaustive study of the two-nucleon systems at a pion mass of \(m_{\pi}\) ∼ 450 MeV.


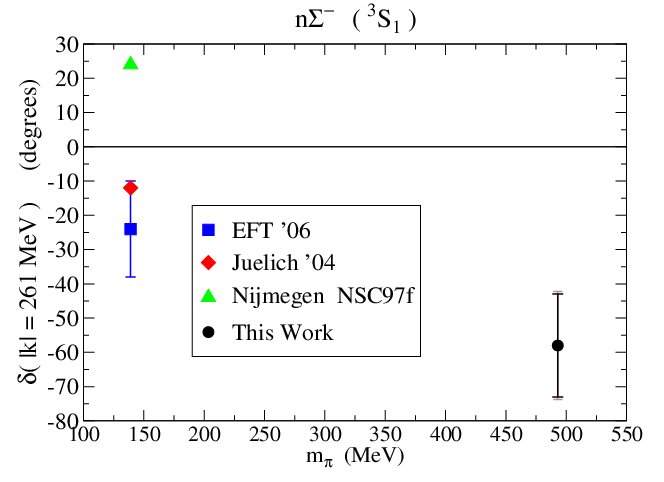
n Sigma- phase shift

Hyperon-Nucleon Scattering

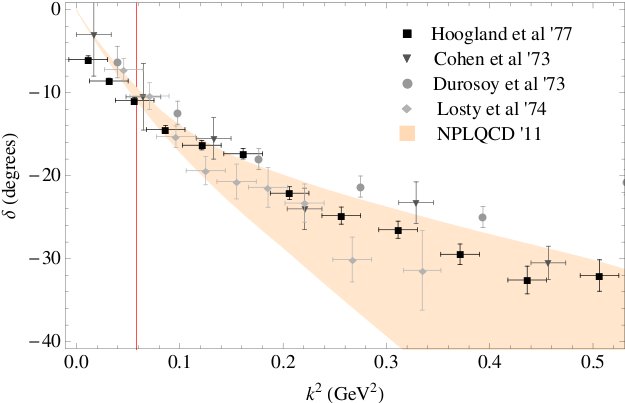
One of the prime objective of the NPLQCD collaboration is to compute scattering amplitudes for processes that are inaccessible, or extremely hard to explore, experimentally. Hyperon-Nucleon scattering may play an important role in the evolution of supernova, but the cross-sections for such processes are very hard to measure, with a grand total of 35 data points exisiting at present. The right plot shows the phase-shift at one energy, in particular our calculation at a pion mass of ~ 500 MeV, compared with theory predictions at the physical pion mass.


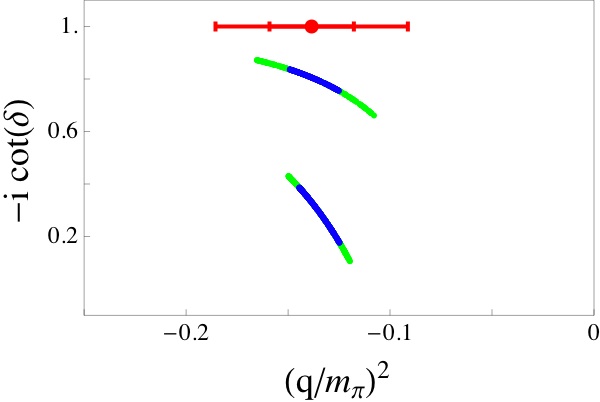
Evidence for a Bound \(H\) Dibaryon

In 2011 we presented evidence for the existence of a bound H-dibaryon, an I=0, J=0, s=-2 state with valence quark structure uuddss. The infinite volume extrapolation of the results of Lattice QCD calculations performed on four ensembles of anisotropic clover gauge-field configurations, with spatial extents of 2.0, 2.5, 3.0 and 3.9 fm at a spatial lattice spacing of 0.123 fm, lead to an H-dibaryon bound by 16.6 ± 2.1 ± 4.6 MeV at a pion mass of 389 MeV. In the figure, the results of the Lattice QCD calculations of \(-i\cot(\delta)\) versus \((q/m_{\pi})^2\) at the two larger lattice sizes, along with the infinite-volume extrapolation (red point). The dark (blue) (light (green)) lines correspond to the statistical (systematic and statistical uncertainties combined in quadrature) 68% confidence intervals calculated.

Featured in Physics: Binding baryons on the lattice


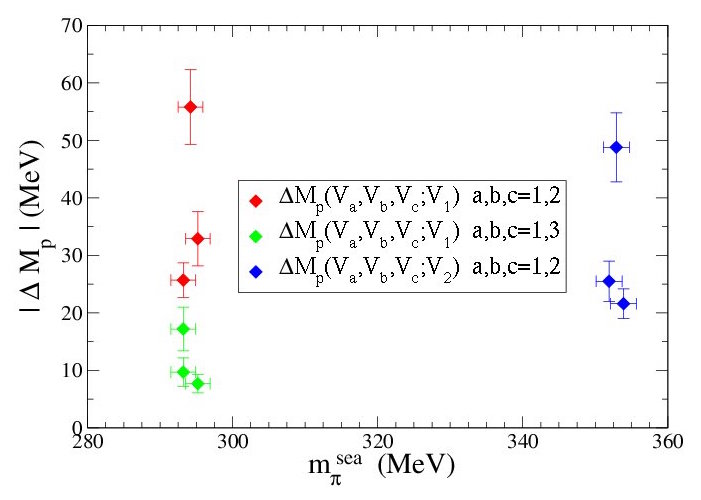
Neutron-Proton Mass-Splitting due to Strong Isospin Breaking - Charge Symmetry Breaking

It is a basic property of our universe that the neutron is slightly more massive than the proton. The electroweak interactions are responsible for this mass difference, which receives contributions from two sources. The strong isospin breaking contribution (also known as charge-symmetry breaking) is due to the difference in the masses of the up and down quarks, ultimately determined by the values of the Yukawa-couplings in the Standard Model of electroweak interactions and the vacuum expectation value of the Higgs field. The other contribution arises from the fact that the proton and neutron carry different electromagnetic charges. The experimental neutron-proton mass difference of \(M_n-M_p = 1.293318 \pm 0.000009\) MeV results from an estimated electromagnetic contribution of \(M_n-M_p = -0.76 \pm 0.30\) MeV and the remaining mass difference is due to a strong isospin breaking contribution of \(M_n-M_p = 2.05 \pm 0.30\) MeV. We calculated \(M_n-M_p = 2.26 \pm 0.57 \pm 0.42 \pm 0.10\) MeV from partially-quenched lattice QCD calculations. The right plot shows the partially-quenched proton mass differences plotted vs the pion mass composed of sea quarks. Various data have been displaced horizontally by small amounts for display purposes.

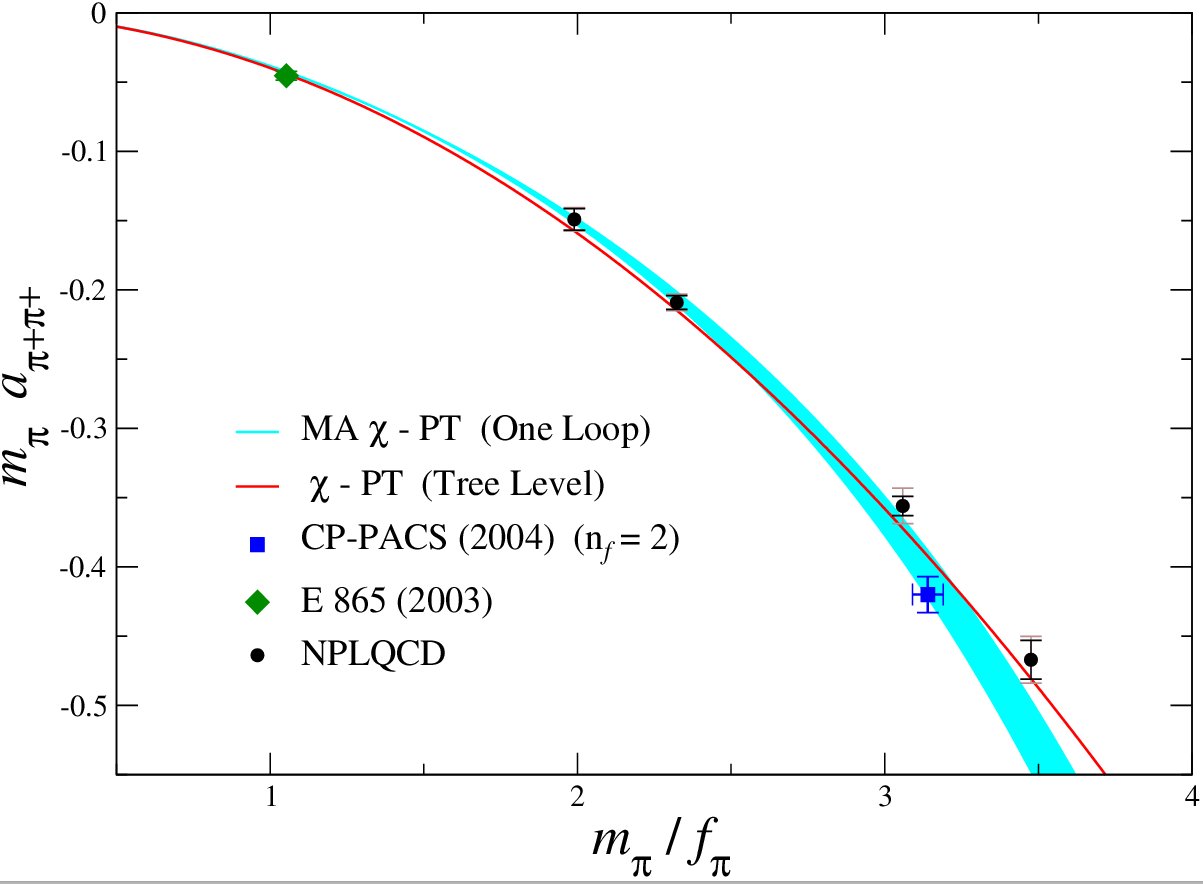
pipi scattering
img

\(\pi\pi\) scattering

The simplest hadronic scattering process is that of two positivly charged pions. Highly constrained by the approximate chiral symmetry of QCD, the scattering length is uniquely predicted at tree-level in chiral perturbation theory [Weinberg--long ago ].
We have calculated this scattering length at the percent level at pion masses down to 290 MeV, and find remarkable agreement with the tree-level prediction of Weinberg, as shown in the right panel. Our prediction for the scattering length at the physical pion mass obtained with one-loop mixed-action chiral perturbation theory is shown along with other determinations/calculations, showing remarkable consistency.


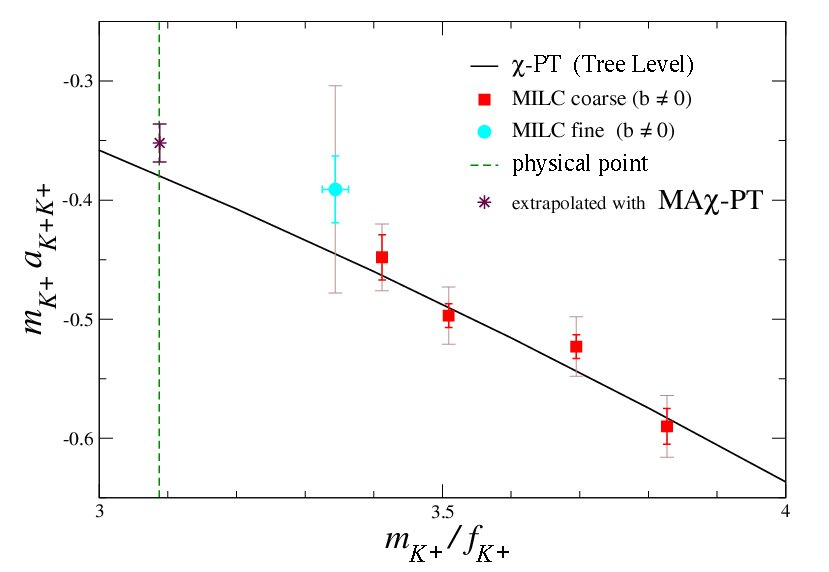
MKAKK verse MK

\(KK\) Scattering

The scattering of two \(K^+\)'s provides a window into the \(n_f\) = 2+1 nature of low-energy QCD. In chiral perturbation theory the counterterms that enters at NLO is the same as that for \(\pi^+\pi^+\) scattering. Surprisingly, the scattering length is seen to be well reproduced by Weinbergs tree-level prediction. This is unexpected as loops were thought to be important at these masses, but apparently are not showing themselves.


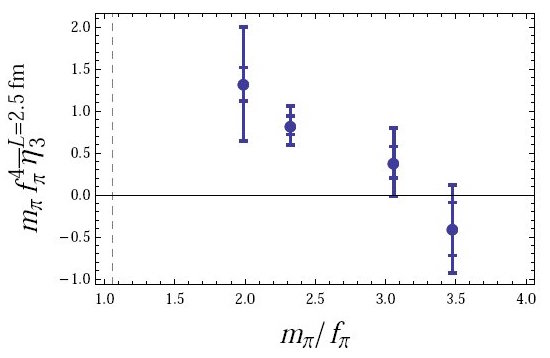
3 body force

Multi-\(\pi\) system

We have recently calculated the energy of multi-pion systems up to and including systems of 12 pions. The first many-body calculation in lattice QCD. The right panel shows the 3-body interaction in NDA units of \(1/m_{\pi} f_{\pi}^4\).


\(f_K / f_{\pi}\)

Lattice determinations of the pseudoscalar decay constants \(f_K\) and \(f_{\pi}\), when combined wityh the experimentally measures branching fractions for \(K \rightarrow \mu \overline{\nu}_{\mu}\gamma\) and \(\pi \rightarrow \mu \overline{\nu}_{\mu}\gamma\) provide important theoretical input into establishing the value of \(V_{us}\), the charged-current matrix element for the \(s \rightarrow u\) transition. Precise determination of \(V_{us}\) and \(V_{ud}\) together with the fact that the square of \(V_{ub}\) is negligibly small, provide a clean test of the tunitarity of the CKM matrix, and thus provide alow-energy probe for physics beyond the standard model with three generations of quarks. We calculated \(f_K / f_{\pi} = 1.218 \pm 0.002^{+0.011}_{-0.024}\).


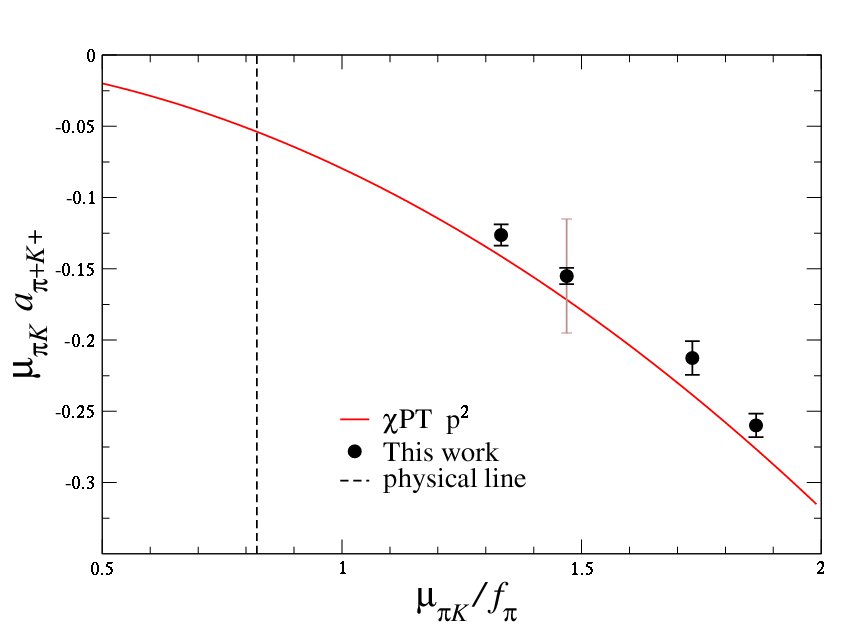
Pi K Scattering

\(\pi K\) scattering

The \(\pi-K\) scattering length is something that is of interest in strong interaction physics as it explores the role of the strange quark in the pseudo-Goldstone sector.The counterterm(s) that contribute at NLO are different from that entering pion-pion and kaon-kaon scattering. We are able to make a remarkably precise prediction for this scattering length.

Magnetic moments

In the past few years, the NPLQCD collaboration has undertaken the first lattice gauge theory computations of the magnetic properties of light nuclei. These include the determination of the magnetic moments and polarizabilities of light nuclei, and the determination of octet baryon magnetic moments. These computations were made possible by two crucial ingredients: the external field technique, for which these properties can be determined from two-point correlation functions rather than three-point functions; and rather large quark masses, for which adequate statistics can be accumulated to provide signal for light nuclei.


First nuclear reaction \(n p \rightarrow d \gamma\)

The first nuclear reaction cross section with direct input from LQCD was reported by the NPLQCD collaboration. The reaction studied was the very low-energy radiative-capture process \(n p \rightarrow d \gamma\), which is dominated by the M1 matrix element. It receives most of its contribution from the nucleon isovector magnetic moment and from correlated two-nucleon interactions with the magnetic field (meson-exchange currents). By performing LQCD calculations at the heavier quark masses, the counterterm in the low-energy EFT describing \(n p \rightarrow d \gamma\) has been determined and extrapolated to the physical point. Using the experimentally measured scattering parameters and the LQCD determined counterterm, the post-dicted \(n p \rightarrow d \gamma\) cross section is found to agree with experiment within the uncertainties.

Double-\(\beta\) decay

In order to complement the searches for the lepton-number violating neutrinoless \(\beta\)\(\beta\)-decay process, it is crucial to constrain, with precision, the relevant nuclear matrix elements. The simpler process of neutrinofull \(\beta\)\(\beta\) decay serves as an important benchmark, and the nuclear many-body techniques have concentrated in improving the matrix-element estimates of this process. With two insertions of the axial current, the background-field method enabled the extraction of this isotensor matrix element at the heavy quark masses of the study, along with a constraint on the short-distance non-Born contribution to the matrix element. This input was used in a pionless EFT description of the double-weak process \(nn \rightarrow pp\) to put bounds, for the first time, on a newly identified short-distance two-axial current two-body coupling, \(\mathbb{H}_{2,S}\) = 4.7(2.2) fm. The contribution arising from this short-distance contribution was found comparable to that from the single-axial current two-body coupling, suggesting that the quenching of \(g_a\) in nuclear many-body calculations of the \(\beta\)\(\beta\)-decay rates might not be sufficient for an accurate determination of the matrix elements.


First calculations of weak reactions

The pp fusion cross section, given its weak strength and the Coulomb barrier between the protons, the rate for this process is currently difficult to measure in experiment. Combined with EFTs (enhanced to account for QED), LQCD input can refine the determination of the short-distance two-body axial-current coupling of the pionless EFT, \(L_{1,A}\). The calculation performed in 2016 with heavy quarks, obtained the matrix element for the axial current in the two-nucleon state with a percent-level uncertainty, and a rough extrapolation was made to the physical point with the assumption of a mild quark-mass dependence in the solely two- body contribution. The result is comparable to the current phenomenological value. Additionally, the Gamov-Teller matrix element contributing to the tritium \(\beta\) decay is obtained from a constraint on the axial charge of \(^3\text{He}\).

Featured in Physics: Strong Force Calculations for Weak Force Reactions

Gluon distribution

The first results on the unpolarized gluon longitudinal momentum fraction in the nucleon and in light nuclei have been computed at a heavy quark mass corresponding to \(m_{\pi}\sim\) 450 MeV and 800 MeV. Such quantity is a signature of the gluonic analog of the EMC effect and is found, from these calculations, to be bounded by ∼ 10 − 20% in light nuclei up to A = 3. The first moment of the gluonic transversity distribution in the deuteron is a clean measure of gluonic degrees of freedom and is protected from the leading-twist mixing with quark distributions. This quantity, is investigated by the NPLQCD collaboration and clear signal was found as heavier pion masses. Such observables, once obtained at the physical values of quark masses, will provide important theoretical input into the designed experiments that aim to explore non-nucleonic gluons in nuclei.