|
1.1 Óptica
Geométrica Paraxial
Subsecciones
1.1.1 Postulados de la Óptica
Geométrica
Definimos el índice de refracción
de un medio  como el
cociente como el
cociente  , donde , donde 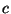 es la velocidad de la luz en el vacío y es la velocidad de la luz en el vacío y
 es la velocidad de la luz en
el medio considerado.
Los cinco postulados de la Óptica Geométrica se enuncian así: es la velocidad de la luz en
el medio considerado.
Los cinco postulados de la Óptica Geométrica se enuncian así:
- Las trayectorias en los medios homogéneos e isótropos
son rectilíneas.
- Sea una superficie que separa dos medios de índices
 y y 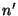 .
El rayo incidente, el reflejado, el transmitido o refractado y la
dirección
normal a la superficie en el punto de incidencia están en el mismo
plano (plano de incidencia). .
El rayo incidente, el reflejado, el transmitido o refractado y la
dirección
normal a la superficie en el punto de incidencia están en el mismo
plano (plano de incidencia).
- Sean
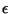 , ,
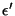 y y  los ángulos que forman el
rayo incidente,
el refractado y el reflejado con la normal, respectivamente. El rayo
incidente
y el transmitido verifican la ley de Snell: los ángulos que forman el
rayo incidente,
el refractado y el reflejado con la normal, respectivamente. El rayo
incidente
y el transmitido verifican la ley de Snell: 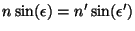 . .
- El rayo incidente y el reflejado verifican la ley de la
reflexión:
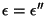 . .
- Las trayectorias de la luz a través de diferentes medios
son
reversibles.
Figura 1.2:Ley
de la reflexión
|
|
1.1.2 Principio de Fermat
Sea un medio homogéneo e isótropo de índice  . La luz viaja entre los puntos A y B,
siguiendo
una trayectoria rectilínea. Definimos el camino óptico . La luz viaja entre los puntos A y B,
siguiendo
una trayectoria rectilínea. Definimos el camino óptico
 como el
producto entre el índice
de refracción y la distancia como el
producto entre el índice
de refracción y la distancia 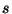 que
recorre la luz entre los dos puntos, que
recorre la luz entre los dos puntos,  . Si la luz
atraviesa
diferentes medios, el camino óptico será . Si la luz
atraviesa
diferentes medios, el camino óptico será
 . . |
(1.1) |
Si el medio es heterogéneo y el índice de
refracción
varía de punto a punto, la definición de camino óptico
se convierte en la siguiente integral
 . . |
(1.2) |
El principio de Fermat dice que para ir de A a B, la luz sigue un
camino extremal (es decir, un camino máximo o mínimo):
 . . |
(1.3) |
1.1.2.1 Teorema de
Malus-Dupin
Si sobre cada rayo que sale de un foco emisor
de luz tomamos caminos ópticos
iguales, los puntos que limitan estos caminos generan una superficie
que es
normal a todos los rayos. Esta superficie se denomina frente de
onda.
1.1.3 Conceptos. Convenio
de signos
1.1.3.1 Sistema óptico
Denominamos sistema óptico a un
conjunto de superficies que
separan medios con índices de refracción diferentes. Si las
superficies son de revolución, y sus centros están alineados,
la recta que los une se denominaeje óptico. El punto emisor
de donde salen los rayos se denomina objeto; el punto donde se
juntan
los rayos, una vez pasado el sistema óptico es la imagen.
Si los rayos pasan físicamente por un punto se denomina real.
El punto es virtual si llegan o salen las prolongaciones de
los rayos.
El conjunto de puntos objeto forma el espacio objeto mientras
que
el conjunto de puntos imagen conforma el espacio imagen.
1.1.3.2 Sistema óptico
perfecto
Un sistema óptico es perfecto si se puede
establecer una relación
de semejanza entre todo el espacio objeto y todo el espacio imagen. Se
puede
demostrar que esta condición no es físicamente viable. Podemos
determinar unas nuevas condiciones menos restrictivas (condiciones de
Maxwell):
- A un plano normal en el eje óptico en el espacio objeto le
corresponde
otro plano normal al eje óptico en el espacio imagen.
- Todos los rayos que entran en el sistema partiendo de un
punto pasan
a la salida por otro punto (real o virtual).
- Toda figura contenida en un plano perpendicular al eje, se
representa
como una figura semejante contenida también en un plano perpendicular
al eje, en el espacio imagen.
Definición de condición de stigmatismo:
Un sistema se
comporta stigmáticamente entre dos puntos cuando todos los rayos que
salen de un punto objeto van a parar a un punto imagen (real o virtual).
1.1.3.3 Convenio de
signos
Figura 1.3:Convenio
de signos.
Variables geométricas
![\includegraphics[width=10cm]{fis2-7.eps}](img31.gif) |
Tabla 1.1:Convenio
de signos. Norma europea
| |
Valor Positivo |
Valor Negativo |
| Distancias a lo largo del eje |
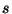 , , 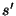 |
Derecha de la superficie |
Izquierda de la superficie |
| Radios de curvatura |
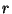 |
Centro a la derecha de la superficie |
Centro a la izquierda de la
superficie |
| Distancias normales al eje |
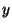 , ,  , , 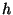 |
Sobre el eje óptico |
Bajo el eje óptico |
| Ángulos de
incidencia, refracción y reflexión |
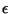 , , 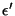 , ,  , ,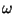 , , 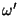 |
Sentido
horario (girando
hacia la normal) |
Sentido
antihorario
(girando hacia la normal) |
| Ángulos con el eje |
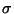 , ,  , ,
 |
Sentido antihorario (girando hacia
el eje óptico) |
Sentido horario (girando hacia el
eje óptico) |
|
1.1.3.4 Óptica paraxial.
Definición
Muchas de las situaciones que se estudian en
la Óptica Geométrica
presentan como particularidad que los ángulos con los cuales se trabaja
son pequeños. Cuando se trabaja en estas condiciones se habla de Óptica
de primer grado o bien Óptica Paraxial. En estos casos,
la aproximación del seno o la tangente del ángulo por su arco
es válida:  , ,  . En estas
condiciones, la ley de la refracción se escribe . En estas
condiciones, la ley de la refracción se escribe
 . .
1.1.4 El Invariante de Abbe
El invariante de Abbe da la
posición de la imagen a partir
de la posición de un punto objeto (emisor) cuando se produce una
refracción a través de una superficie esférica de radio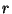 que separa dos medios de índices que separa dos medios de índices
 y y 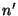 ; ;
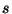 y y 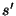 son las distancias del objeto a la superficie y de ésta a la imagen,
respectivamente. La fórmula del invariante de Abbe indica que cualquier
par de puntos objeto-imagen verifica la relación de stigmatismo. Esta
relación es válida en condiciones paraxiales.
son las distancias del objeto a la superficie y de ésta a la imagen,
respectivamente. La fórmula del invariante de Abbe indica que cualquier
par de puntos objeto-imagen verifica la relación de stigmatismo. Esta
relación es válida en condiciones paraxiales.
 . . |
(1.4) |
Esta fórmula se puede aplicar repetidamente para varias superficies
aplicando la fórmula de paso:
 , , |
(1.5) |
que relaciona las distancias imagen y objeto de superficies
consecutivas.
Figura 1.4:
Fórmula de
paso entre dos superficies
![\includegraphics[width=8cm, height=4cm]{fpas.eps}](img47.gif) |
Si la superficie es un espejo, entonces  y la fomula se escribe y la fomula se escribe
 . . |
(1.6) |
1.1.5 Aumentos. Planos focales
y principales
1.1.5.1 Aumento lateral
Se define el aumento como la
relación de tamaño entre
la imagen y el objeto:  .
Para
un sistema con .
Para
un sistema con 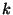 superficies
que
separan superficies
que
separan  medios, el
aumento se puede
calcular como medios, el
aumento se puede
calcular como
 , , |
(1.7) |
donde  y y  son las distancias objeto e
imagen parciales referidas
a la superficie son las distancias objeto e
imagen parciales referidas
a la superficie  . .
1.1.5.2 Planos focales y
planos principales
- El punto del eje óptico donde se cortan los rayos que
provienen
del infinito y que son paralelos al eje óptico se denomina foco
imagen. De forma análoga, el punto del eje óptico que tiene
por imagen el infinito se denomina foco objeto.
- El plano perpendicular al eje óptico que contiene el foco o
punto
focal se denominaplano focal. Los rayos que provienen del
infinito
y que entran en el sistema óptico formando un cierto ángulo
con el eje óptico se cruzan en un punto del plano focal.
- Denominamos planos principales a dos planos
conjugados perpendiculares al eje con aumento lateral
 entre ellos. El punto de intersección entre las prolongaciones
del rayo procedente del infinito, y que es paralelo al eje óptico, y
del rayo que a la salida va a buscar el foco, marcan la posición
del plano principal imagen
entre ellos. El punto de intersección entre las prolongaciones
del rayo procedente del infinito, y que es paralelo al eje óptico, y
del rayo que a la salida va a buscar el foco, marcan la posición
del plano principal imagen  .
El plano principal objeto .
El plano principal objeto  se
encuentra
de forma análoga, considerando un rayo que pasa por el foco objeto.
El conocimiento de los planos principales y focales nos da toda la
información
necesaria para el estudio de un sistema óptico en primer orden
con independencia de su complejidad. se
encuentra
de forma análoga, considerando un rayo que pasa por el foco objeto.
El conocimiento de los planos principales y focales nos da toda la
información
necesaria para el estudio de un sistema óptico en primer orden
con independencia de su complejidad.
- La distancia entre los planos principales y focales se
denomina distancia focal o simplemente focal. Las
focales objeto y imagen verifican la relación
 . . |
(1.8) |
- En una superficie esférica, los planos principales
 y y  se confunden con propia superficie esférica (fijémonos que estamos
en aproximación paraxial). Las focales se pueden calcular utilizando
el invariante de Abbe:
se confunden con propia superficie esférica (fijémonos que estamos
en aproximación paraxial). Las focales se pueden calcular utilizando
el invariante de Abbe:
 . . |
(1.9) |
- El inverso de la distancia focal imagen se denomina potencia
de un sistema óptico
 y se mide en dioptrías (1
y se mide en dioptrías (1 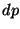 =
1 =
1  ). ).
1.1.6 Ley de las lentes
Figura 1.5:
Ley de las lentes
![\includegraphics[width=10cm]{fis2-18.eps}](img65.gif) |
En un sistema óptico definido por las
posiciones de los planos principales
y focales, se verifican las siguientes relaciones
 , , |
(1.10) |
donde 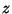 es la posición del objeto
referidada al foco objeto y es la posición del objeto
referidada al foco objeto y  es la posición de la imagen referidada al foco imagen. Si los índices
extremos son iguales, caso habitual en las lentes y los instrumentos
ópticos,
es la posición de la imagen referidada al foco imagen. Si los índices
extremos son iguales, caso habitual en las lentes y los instrumentos
ópticos,
 , ,
 . . |
(1.11) |
En este caso, el aumento lateral es  . .
1.1.7 Sistemas compuestos
Tenemos dos sistemas ópticos bien definidos
por sus planos principales
y focales, dispuestos según se indica en la figura 1.6. Se puede demostrar que es posible
determinar
un único sistema (sistema compuesto) de planos principales
y focales conjuntos, calculados a partir de los de cada sistema. Por lo
general,
cualquier sistema óptico, con independencia de su complejidad, puede
ser reducido a un único par de planos principales y focales. Esto
supone
una notable simplificación en el estudio paraxial de sistemas ópticos
complejos, ie. formados por muchas lentes o espejos.
Figura 1.6:Sistemas
compuestos
![\includegraphics[width=10cm]{fis2-19.eps}](img72.gif) |
A continuación se indican las fórmulas que
permiten obtener
la focal conjunta del sistema compuesto, así como las posiciones
de sus planos principales y focales:
Tabla 1.2:Fórmulas
de acoplamiento de sistemas
|
|
1.1.8 Lentes
Las lentes son la base de los instrumentos
ópticos. Están formadas
por dos superficies refractivas (que aquí tomaremos esféricas
de radios  y y  ), separadas una distancia ), separadas una distancia 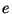 , que encierran un medio de índice , que encierran un medio de índice  . Podemos estudiar su funcionamiento
considerándolas
como sistemas compuestos, puesto que a cada superficie esférica le
podemos asignar sus planos principales y focales asociados. Aplicando
las
fórmulas de los sistemas compuestos podemos determinar estos valores.
Sean . Podemos estudiar su funcionamiento
considerándolas
como sistemas compuestos, puesto que a cada superficie esférica le
podemos asignar sus planos principales y focales asociados. Aplicando
las
fórmulas de los sistemas compuestos podemos determinar estos valores.
Sean  y y  los índices de los medios inicial y final y los índices de los medios inicial y final y , el índice del material del cual
está hecha la lente: , el índice del material del cual
está hecha la lente:
Tabla 1.3:Fórmulas
de diseño
de lentes
Caso general,  , ,  , ,  diferentes diferentes |
Índices extremos aire  |
 |
![$\frac{1}{f'}
= (n-1) \left [\frac{1}{r_1}-\frac{1}{r_2} \right ] + \frac{(n-1)^2}{n}
\frac{e}{r_1 r_2}$](img88.gif) |
 |
 |
 |
 |
|
1.1.8.1 Lentes delgadas
Si el grosor de la lente es pequeño frente a
los radios de curvatura
y  , se verifica
que , se verifica
que
![\begin{displaymath}
\frac{1}{f'} = (n-1) \left [\frac{1}{r_1}-\frac{1}{r_2} \right ] \quad
H_1H=0 \quad H_2'H'=0
\vspace{5mm}
\end{displaymath}](img93.gif) . . |
(1.12) |
1.1.9 Formación de imágenes en una lente
Fórmula de formación de imágenes en las
lentes (índices extremos iguales): 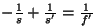 . .
Figura 1.7:
Gráfica  para una lente
convergente de para una lente
convergente de  m m
|
|
Figura 1.8:
Lente convergente.
Objeto real e imagen real
![\includegraphics[width=10cm]{form0c1.eps}](img96.gif) |
Figura 1.9:
Lente convergente.
Objeto real e imagen virtual
![\includegraphics[width=10cm]{form0c2.eps}](img97.gif) |
Figura 1.10:
Lente convergente.
Objeto virtual e imagen real
![\includegraphics[width=10cm]{form0c3.eps}](img98.gif) |
Figura 1.11:
Gráfica  para una lente
divergente de para una lente
divergente de  m m
|
|
Figura 1.12:
Lente divergente.
Objeto real e imagen virtual
![\includegraphics[width=10cm]{form0d1.eps}](img100.gif) |
Figura 1.13:
Lente divergente.
Objeto virtual e imagen real
![\includegraphics[width=10cm]{form0d2.eps}](img101.gif) |
Figura 1.14:Lente
divergente. Objeto
virtual e imagen virtual
![\includegraphics[width=10cm]{form0d3.eps}](img102.gif) |
1.1.10 Formación
de imágenes en un espejo esférico
Fórmula de formación de imágenes en espejos
esféricos:
 . .
Figura 1.15:
Gráfica  para un espejo
esférico convexo
de para un espejo
esférico convexo
de  m m
|
|
Figura 1.16:Espejo
esférico
convexo. Objeto real e imagen virtual
|
|
Figura 1.17:Espejo
esférico
convexo. Objeto virtual e imagen real
|
|
Figura 1.18:Espejo
esférico
convexo. Objeto virtual e imagen virtual
|
|
Figura 1.19:
Gráfica  para un espejo
esférico cóncavo
de para un espejo
esférico cóncavo
de  m m
|
|
Figura 1.20:Espejo
esférico
cóncavo. Objeto real e imagen real
|
|
Figura 1.21:
Espejo esférico cóncavo. Objeto real e imagen virtual
|
|
Figura 1.22:
Espejo esférico cóncavo. Objeto virtual e imagen real
|
|
1.1.11 Limitaciones de luz
y campo en sistemas ópticos
- Diafragma de apertura. Dado un sistema óptico, el
elemento
que limita la cantidad de luz que atraviesa el sistema (montura de
lente,
diafragma intercalado, ...) se denomina diafragma de apertura.
Su
imagen en el espacio objeto, que indica la medida de la apertura por
donde
penetra la luz, recibe el nombre de pupila de entrada. La
imagen
del diafragma de apertura en el espacio imagen, que indica la medida de
la
apertura por donde sale la luz, recibe el nombre de pupila de
salida.
- Diafragma de campo. Dado un sistema óptico, el
elemento
que limita el tamaño del objeto se denomina diafragma de campo.
Su imagen en el espacio objeto recibe el nombre de lucarna de
entrada.
La imagen del diafragma de campo en el espacio imagen, recibe el nombre
de lucarna de salida.
|

