| |
3.1 Coherencia
Subsecciones
3.1.1 Coherencia temporal
y monocromaticidad
Un sistema físico aislado (piénsese
en un átomo,
por ejemplo), con sus niveles energéticos perfectamente definidos,
es una idealización que permite explicar la existencia de ondas
monocromáticas.
Si este sistema se encuentra en el nivel de energía 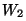 y pasa a un estado de energía y pasa a un estado de energía
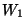 tal que tal que 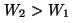 , la física cuantica predice que se genera
un fotón cuya longitud de onda verifica , la física cuantica predice que se genera
un fotón cuya longitud de onda verifica 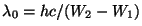 , donde , donde 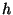 es la constante de Planck. Si el sistema
considerado no es ideal, sus niveles energéticos pueden estar
degenerados,
y los fotones que se emitan, tendrán una longitud de onda que fluctuará
en el intervalo es la constante de Planck. Si el sistema
considerado no es ideal, sus niveles energéticos pueden estar
degenerados,
y los fotones que se emitan, tendrán una longitud de onda que fluctuará
en el intervalo ![$[\lambda_0 - \Delta \lambda,
\lambda_0 + \Delta \lambda]$](img479.gif) .
Además, las transiciones energéticas posibles entre la banda
de energía 2 y la banda 1 no tienen que ser equiprobables. Podemos
definir, por lo tanto, una distribución .
Además, las transiciones energéticas posibles entre la banda
de energía 2 y la banda 1 no tienen que ser equiprobables. Podemos
definir, por lo tanto, una distribución 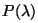 que indique la probabilidad de generar un fotón
con una cierta longitud de onda. Algunas causas que hacen que los
niveles
energéticos estén degenerados pueden ser el efecto Doppler
como consecuencia de la agitación térmica o bien las colisiones
entre las partículas que formen el material. En estos casos, la forma
de que indique la probabilidad de generar un fotón
con una cierta longitud de onda. Algunas causas que hacen que los
niveles
energéticos estén degenerados pueden ser el efecto Doppler
como consecuencia de la agitación térmica o bien las colisiones
entre las partículas que formen el material. En estos casos, la forma
de 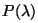 es
aproximadamente como la que
muestra la figura 3.1,
mientras que en el
caso ideal es
aproximadamente como la que
muestra la figura 3.1,
mientras que en el
caso ideal 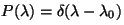 . .
Figura 3.1:
Distribución 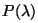
|
|
El campo eléctrico asociado a una onda plana
ideal es 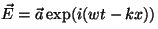 , donde
la amplitud , donde
la amplitud 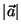 será
constante, en valor y dirección. En el caso no ideal, la onda que
obtendremos se escribirá como superposición (suma) de ondas
monocromáticas, es decir: será
constante, en valor y dirección. En el caso no ideal, la onda que
obtendremos se escribirá como superposición (suma) de ondas
monocromáticas, es decir:
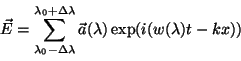 , , |
(3.1) |
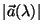 se relaciona directamente
con se relaciona directamente
con
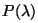 y, si la
longitud de onda en
el sumatorio anterior es una variable continua, la ecuación anterior
se convertirá en una integral. Un análisis en profundidad de
las matemáticas involucradas en la expresión anterior nos aportará
un resultado muy interesante: una onda real, suma de diferentes
contribuciones
monocromáticas, está limitada en el espacio y constituye lo
que se denomina un paquete de ondas. La longitud física del paquete
de ondas se denomina longitud de coherencia, y, si la
longitud de onda en
el sumatorio anterior es una variable continua, la ecuación anterior
se convertirá en una integral. Un análisis en profundidad de
las matemáticas involucradas en la expresión anterior nos aportará
un resultado muy interesante: una onda real, suma de diferentes
contribuciones
monocromáticas, está limitada en el espacio y constituye lo
que se denomina un paquete de ondas. La longitud física del paquete
de ondas se denomina longitud de coherencia, 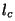 (véanse figuras 3.2
y 3.3). Cuando
más monocromática es la onda (es decir, cuando más estrecha
sea la distribución (véanse figuras 3.2
y 3.3). Cuando
más monocromática es la onda (es decir, cuando más estrecha
sea la distribución 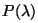 de la figura 3.1) mayor es
de la figura 3.1) mayor es 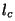 : en el límite, una onda plana
es perfectamente monocromática y su longitud de coherencia es infinita. : en el límite, una onda plana
es perfectamente monocromática y su longitud de coherencia es infinita.
Figura 3.2:
Longitud de coherencia finita
![\includegraphics[width=\linewidth, height=5cm]{loncohinf.ps}](img487.gif) |
Figura 3.3:
Longitud de coherencia infinita: onda plana
![\includegraphics[width=\linewidth, height=5cm]{loncohfin.ps}](img488.gif) |
Cuando se genera un paquete de ondas, se
introduce una fase inicial aleatoria
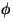 . Dos paquetes de ondas
tendrán
fases iniciales diferentes. Es necesario utilizar iluminación láser
en los experimentos de interferencias para evitar los problemas
derivados
de la coherencia. Los láseres presentan una alta monocromaticidad,
y, por lo tanto, sus longitudes de coherencia son muy elevadas. . Dos paquetes de ondas
tendrán
fases iniciales diferentes. Es necesario utilizar iluminación láser
en los experimentos de interferencias para evitar los problemas
derivados
de la coherencia. Los láseres presentan una alta monocromaticidad,
y, por lo tanto, sus longitudes de coherencia son muy elevadas.
3.1.2 Condiciones para obtener
imágenes de interferencia estables
En general, cuando dos ondas 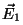 y
y 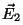 se encuentran en
el espacio,
no interaccionan de forma apreciable. Ahora bien, si se verifican unas
determinadas
condiciones, estas ondas pueden generar una distribución de intensidad
con zonas donde la energía se potencia y otras en las que la energía
disminuye. Las condiciones para obtener imágenes de interferencia
estables son cuatro: se encuentran en
el espacio,
no interaccionan de forma apreciable. Ahora bien, si se verifican unas
determinadas
condiciones, estas ondas pueden generar una distribución de intensidad
con zonas donde la energía se potencia y otras en las que la energía
disminuye. Las condiciones para obtener imágenes de interferencia
estables son cuatro:
- Las ondas que interfieren deben ser coherentes.
- Las ondas deben tener la misma frecuencia.
- Los campos eléctricos deben ser paralelos.
- Las amplitudes de los campos deben ser iguales.
Tomamos dos ondas planas de polarización,
amplitud, frecuencia, fase
inicial y dirección de propagación diferentes, que se superponen
en un punto del espacio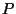 : :
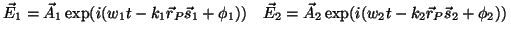 . . |
(3.2) |
Si captamos la intensidad en este punto  tendremos tendremos
 , , |
(3.3) |
y desarrollando,
donde 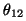 es el ángulo
formado por los dos vectores campo eléctrico. Esta intensidad es
función
del tiempo. Las variaciones que presenta esta función serán
muy rápidas en el rango de las frecuencias ópticas. Por lo
tanto, la magnitud que se detectará será la media temporal
de la intensidad. Para apreciar fenómenos interferenciales deben
cumplirse las condiciones expuestas anteriormente: es el ángulo
formado por los dos vectores campo eléctrico. Esta intensidad es
función
del tiempo. Las variaciones que presenta esta función serán
muy rápidas en el rango de las frecuencias ópticas. Por lo
tanto, la magnitud que se detectará será la media temporal
de la intensidad. Para apreciar fenómenos interferenciales deben
cumplirse las condiciones expuestas anteriormente:
- Las ondas que interfieren deben ser coherentes
entre si.
Si los dos haces de luz que interactúan son incoherentes, las fases
iniciales asociadas a cada onda irán cambiando aleatoriamente.
Por lo tanto, la diferencia
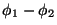 que aparece en los términos cruzados
de la ecuación 3.4
variará
aleatoriamente. Puesto que la media temporal de una fase que varía
al azar es nula, los términos cruzados de la ecuación 3.4 también serán
nulos.
Este problema se evita cuando la diferencia
que aparece en los términos cruzados
de la ecuación 3.4
variará
aleatoriamente. Puesto que la media temporal de una fase que varía
al azar es nula, los términos cruzados de la ecuación 3.4 también serán
nulos.
Este problema se evita cuando la diferencia 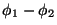 es constante en el tiempo, es decir,
cuando
los paquetes de onda son coherentes. Esto se consigue a partir de un
único haz de luz, dividiéndolo en dos y haciendo que cada
uno acumule un camino óptico diferente. Los dos haces resultantes
llegarán con un determinado desfase. Si la diferencia de camino
óptico es inferior a la longitud de coherencia, durante una fracción
de tiempo se verificará la condición es constante en el tiempo, es decir,
cuando
los paquetes de onda son coherentes. Esto se consigue a partir de un
único haz de luz, dividiéndolo en dos y haciendo que cada
uno acumule un camino óptico diferente. Los dos haces resultantes
llegarán con un determinado desfase. Si la diferencia de camino
óptico es inferior a la longitud de coherencia, durante una fracción
de tiempo se verificará la condición 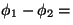 constante y los
dos paquetes de onda se superpondrán parcialmente (véase
la figura 3.4). Los paquetes de onda
que
vengan a continuación también se superpondrán. Cuanto más largos sean
los paquetes de onda y más se superpongan, los fenómenos
interferenciales se observarán con mayor facilidad. constante y los
dos paquetes de onda se superpondrán parcialmente (véase
la figura 3.4). Los paquetes de onda
que
vengan a continuación también se superpondrán. Cuanto más largos sean
los paquetes de onda y más se superpongan, los fenómenos
interferenciales se observarán con mayor facilidad.
-
Figura 3.4:
Superposición parcial de a dos paquetes de onda
|
![\includegraphics[width=12cm, height=5cm]{supcoh.ps}](img502.gif) |
- Las ondas deben tener la misma
frecuencia. Si
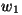 y y  son diferentes, la intensidad dependerá
del tiempo
y, en este caso, la media temporal también será cero. son diferentes, la intensidad dependerá
del tiempo
y, en este caso, la media temporal también será cero.
- Los campos eléctricos deben ser
paralelos. Si
los campos eléctricos no son paralelos, el término
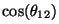 actuará haciendo
que los términos cruzados tengan una importancia menor respeto los
términos constantes actuará haciendo
que los términos cruzados tengan una importancia menor respeto los
términos constantes 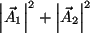 . En particular,
cuando las polarizaciones están en cuadratura, los
términos cruzados desaparecen. Éste es el caso que corresponde
al estudio de la luz polarizada. Si . En particular,
cuando las polarizaciones están en cuadratura, los
términos cruzados desaparecen. Éste es el caso que corresponde
al estudio de la luz polarizada. Si 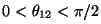 , se superpone
luz polarizada a las interferencias. La visualización de fenómenos
interferenciales se optimiza cuando los campos eléctricos son
estrictamente paralelos. La ecuación 3.4
de la intensidad, se escribe ahora (se
verifica la condición de coherencia, la igualdad de frecuencias y el
paralelismo de los campos) , se superpone
luz polarizada a las interferencias. La visualización de fenómenos
interferenciales se optimiza cuando los campos eléctricos son
estrictamente paralelos. La ecuación 3.4
de la intensidad, se escribe ahora (se
verifica la condición de coherencia, la igualdad de frecuencias y el
paralelismo de los campos)
-
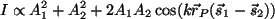 . . |
(3.5) |
Se ha prescindido del carácter vectorial de los campos para escribir
las amplitudes. Esto es posible ya que se ha impuesto que los campos
eléctricos deben tener todos la misma dirección. La polarización es
una información que no aporta nada a la física del problema.
Los planteamientos en óptica donde la dirección de polarización
no es una información relevante conforman una parte de la óptica
que se denomina teoría escalar de la luz.
- Las amplitudes de los campos deben
ser iguales: Si
además, la amplitud los campos es la misma, (
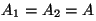 ), entonces la distribución
de intensidad se escribe ), entonces la distribución
de intensidad se escribe
-
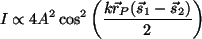 . . |
(3.6) |
Cuando se verifican las dos primeras condiciones, la figura de
interferencia es estable. Si además se asegura el paralelismo de los
campos,
se puede observar claramente el comportamiento interferencial. La
distribución de intensidad tiene un contraste óptimo cuando, además,
las amplitudes de las dos ondas que interaccionas son iguales.
|

