|
2.1
Ondas electromagnéticas
Subsecciones
2.1.1 Ecuaciones de Maxwell
El formalismo básico para describir los
fenómenos electromagnéticos
relacionados con la óptica ondulatoria son las ecuaciones de Maxwell.
En el sistema CGS Gauss se escriben como:
|
|
(2.1) |
|
|
|
|
 , |
donde 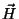 es el campo
magnético, es el campo
magnético,
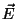 es el campo
eléctrico, es el campo
eléctrico, 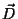 es el vector
desplazamiento, es el vector
desplazamiento, 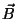 es el vector inducción magnética,
es el vector inducción magnética,
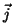 es la densidad
de corriente, es la densidad
de corriente, 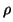 es la densidad
de carga y es la densidad
de carga y 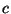 es una
constante de proporcionalidad.
Las ecuaciones de Maxwell se complementan con las denominadas
relaciones
constitutivas: es una
constante de proporcionalidad.
Las ecuaciones de Maxwell se complementan con las denominadas
relaciones
constitutivas:
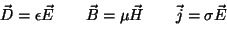 , , |
(2.2) |
donde 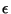 es la
constante dieléctrica, es la
constante dieléctrica,
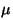 es la permeabilidad
magnética
y es la permeabilidad
magnética
y 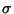 es la conductividad
eléctrica.
En un medio dieléctrico homogéneo, isótropo y sin carga, es la conductividad
eléctrica.
En un medio dieléctrico homogéneo, isótropo y sin carga,
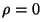 , , 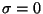 , , 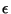 y
y 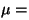 constantes. Las ecuaciones
se simplifican: constantes. Las ecuaciones
se simplifican:
Cuando un campo electromagnético cambia de
medio, las componentes
normales y tangenciales de éste verifican las relaciones siguientes:
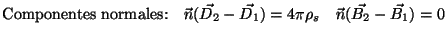 |
(2.4) |
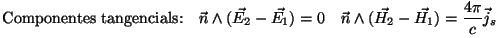 , , |
donde 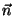 es el vector
normal
a la superficie, y es el vector
normal
a la superficie, y 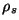 y
y 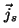 son las
densidades superficiales
de carga y de corriente, respectivamente. Los subíndices 1 y 2 hacen
referencia a los campos en el medio original y en el medio en el que se
transmiten los campos, respectivamente. Si las densidades de carga y
corriente
son cero, son las
densidades superficiales
de carga y de corriente, respectivamente. Los subíndices 1 y 2 hacen
referencia a los campos en el medio original y en el medio en el que se
transmiten los campos, respectivamente. Si las densidades de carga y
corriente
son cero, 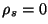 y y 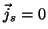 , entonces se verifican
las siguientes relaciones de continuidad: , entonces se verifican
las siguientes relaciones de continuidad:
 |
(2.5) |
 . . |
Los superíndices  y y 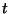 hacen referencia a las componentes normales
o tangenciales.
hacen referencia a las componentes normales
o tangenciales.
2.1.2
La ecuación
de ondas. Soluciones
En un medio homogéneo e isótropo, al combinar
las ecuaciones
de Maxwell se obtiene el par de ecuaciones siguiente:
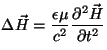 |
(2.6) |
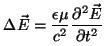 . . |
Estas expresiones son formalmente ecuaciones de ondas. Así, la
velocidad
de propagación puede relacionarse con los parámetros 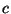 , , 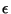 y
y 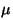
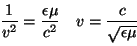 . . |
(2.7) |
En el vacío, 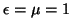 , y por lo tanto , y por lo tanto 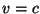 . Es decir, . Es decir, 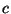 es
la velocidad de la luz en el vacío. El índice
de refracción se puede escribir en función de los parámetros es
la velocidad de la luz en el vacío. El índice
de refracción se puede escribir en función de los parámetros
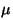 y y 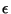 , , 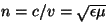 . Sean . Sean 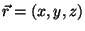 el vector posición
de un punto y el vector posición
de un punto y 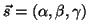 el vector
unitario ( el vector
unitario ( 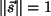 ) que indica la dirección de
propagación de la onda. Se puede comprobar fácilmente que
una función ) que indica la dirección de
propagación de la onda. Se puede comprobar fácilmente que
una función 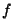 del tipo del tipo 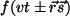 es solución
de la ecuación de ondas. Esta solución de la ecuación
de ondas se denomina onda plana. En el caso unidimensional,
escribiremos
la ecuación de ondas como es solución
de la ecuación de ondas. Esta solución de la ecuación
de ondas se denomina onda plana. En el caso unidimensional,
escribiremos
la ecuación de ondas como
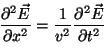 . . |
(2.8) |
En este caso particular,  , y la solución
se escribe como , y la solución
se escribe como 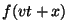 o
o 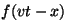 . De las
relaciones entre la pulsación . De las
relaciones entre la pulsación
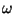 , el periodo , el periodo 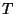 , , 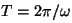 , la longitud de onda , la longitud de onda 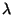 , el número de onda , el número de onda 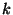 , , 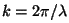 , la longitud de
onda,
la frecuencia , la longitud de
onda,
la frecuencia 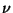 y la
velocidad, y la
velocidad,
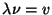 , podemos escribir el argumento de la
función
de onda plana como: , podemos escribir el argumento de la
función
de onda plana como:
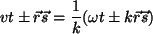 . . |
(2.9) |
Dependiendo del caso que se estudie, la función 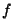 puede ser complicada de describir. El
análisis de Fourier afirma que cualquier función
puede ser descrita como una combinación lineal de funciones armónicas.
Por esta razón, tomaremos funciones de onda armónicas para
describir los campos eléctrico y magnético, por ejemplo: puede ser complicada de describir. El
análisis de Fourier afirma que cualquier función
puede ser descrita como una combinación lineal de funciones armónicas.
Por esta razón, tomaremos funciones de onda armónicas para
describir los campos eléctrico y magnético, por ejemplo:
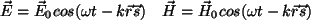 , , |
(2.10) |
donde los módulos 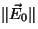 y y 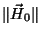 son las
amplitudes
máximas de los campos eléctrico y magnético, respectivamente.
El argumento de estas funciones es adimensional. Por comodidad, a la
hora
de hacer manipulaciones matemáticas, escribiremos los campos en
notación
compleja, aunque únicamente la parte real (o la imaginaria) tiene
sentido físico, es decir: son las
amplitudes
máximas de los campos eléctrico y magnético, respectivamente.
El argumento de estas funciones es adimensional. Por comodidad, a la
hora
de hacer manipulaciones matemáticas, escribiremos los campos en
notación
compleja, aunque únicamente la parte real (o la imaginaria) tiene
sentido físico, es decir:
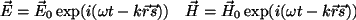 , , |
(2.11) |
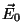 es la amplitud
de la onda y es la amplitud
de la onda y
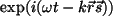 su fase, que también se puede escribir
en términos del índice
de refracción. Si definimos su fase, que también se puede escribir
en términos del índice
de refracción. Si definimos 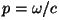 ,
tendremos que ,
tendremos que
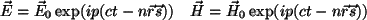 . . |
(2.12) |
Definimos el concepto de frente de onda como el lugar
geométrico
de los puntos que tienen la misma fase, en un momento dado. En el caso
de
ondas planas, el frente de onda es el plano 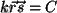 donde donde 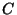 es una constante. Es posible establecer
una relación entre los conceptos de fase y camino óptico
( es una constante. Es posible establecer
una relación entre los conceptos de fase y camino óptico
(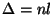 , donde , donde  es el índice de refracción
y es el índice de refracción
y 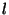 la distancia recorrida por
la onda). Sea una onda de pulsación la distancia recorrida por
la onda). Sea una onda de pulsación 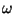 y dirección de propagación y dirección de propagación 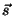 . La diferencia de fase entre dos
planos ` . La diferencia de fase entre dos
planos `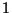 ' y ` ' y `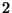 ' del frente de onda, distantes ' del frente de onda, distantes 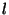 entre si, es entre si, es
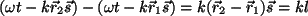 . . |
(2.13) |
Si la onda se propaga en un medio de índice  , , 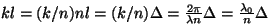 .
Este resultado se utilizará más adelante en el estudio de los
sistemas interferenciales. Otra solución de la ecuación de
onda que presenta un gran interés es aquella en la que el valor de
la amplitud de la onda sólo depende de la distancia al punto en que
se genera. En este caso (onda esférica), es conveniente escribir
la ecuación en coordenadas esféricas y quedarnos solo con
la parte radial, es decir, .
Este resultado se utilizará más adelante en el estudio de los
sistemas interferenciales. Otra solución de la ecuación de
onda que presenta un gran interés es aquella en la que el valor de
la amplitud de la onda sólo depende de la distancia al punto en que
se genera. En este caso (onda esférica), es conveniente escribir
la ecuación en coordenadas esféricas y quedarnos solo con
la parte radial, es decir, 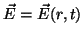 : :
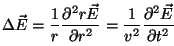 , , |
(2.14) |
y así podemos escribir
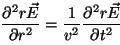 . . |
(2.15) |
Esta última expresión es formalmente idéntica a la ecuación
de ondas en una dimensión escrita en coordenadas cartesianas. Por
lo tanto, la solución en este caso será del tipo
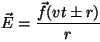 . . |
(2.16) |
Aquí el frente de ondas es una esfera.
Figura 2.1:
Diferencia de fase
![\includegraphics[width=\linewidth]{Diffase.eps}](img226.gif) |
Figura 2.2:
Diferencia de fase
(esquema transversal)
![\includegraphics[width=\linewidth]{Diffase2.eps}](img227.gif) |
2.1.3
Energía. Vector
de Poynting
Introduciendo las soluciones de la ecuación
de ondas para los campos
eléctrico y magnético en las ecuaciones de Maxwell, podemos
deducir las relaciones siguientes :
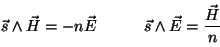 , , |
(2.17) |
relaciones que indican que los vectores campo eléctrico, campo
magnético
y el vector 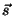 son
ortogonales entre si. Los vectores campos eléctrico y magnético
vibran en un plano que se propaga según la dirección son
ortogonales entre si. Los vectores campos eléctrico y magnético
vibran en un plano que se propaga según la dirección 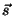 , tal y como se muestra en la figura
2.3. La energía
electromagnética
almacenada en un diferencial de volumen se escribe , tal y como se muestra en la figura
2.3. La energía
electromagnética
almacenada en un diferencial de volumen se escribe
![\begin{displaymath}
du = \left [ \frac{1}{8 \pi} (\epsilon \Vert {\vec E}\Vert^2 + \mu \Vert
{\vec H}\Vert^2) \right ] dv
\vspace{5mm}
\end{displaymath}](img229.gif) , , |
(2.18) |
y por lo tanto, la variación por unidad de tiempo de energía
electromagnética almacenada en un volumen V cerrado por una superficie
S es
![\begin{displaymath}
\frac{\partial u }{\partial t}= \frac{\partial}{\partial t}...
...mu \Vert {\vec
H}\Vert^2) \right ] \right ] dv
\vspace{5mm}
\end{displaymath}](img230.gif) . . |
(2.19) |
Figura 2.3:
Transversalidad
de los campos eléctrico y magnético
|
|
Consideremos un material dieléctrico ideal (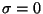 ). Utilizando las ecuaciones
de Maxwell podemos
demostrar que la variación de energía puede expresarse como ). Utilizando las ecuaciones
de Maxwell podemos
demostrar que la variación de energía puede expresarse como
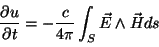 . . |
(2.20) |
Definimos el vector de Poynting como
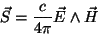 . . |
(2.21) |
El vector de Poynting expresa la variación de energía radiada
por unidad de tiempo y de superficie perpendicular a la dirección
de propagación. En los medios homogéneos e isótropos
el vector de Poynting y el vector 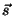 tienen la misma dirección. La dirección del rayo (concepto
propio de la Óptica Geométrica) y
tienen la misma dirección. La dirección del rayo (concepto
propio de la Óptica Geométrica) y 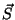 (asociado a la propagación de la energía
de la onda) coinciden. Si la longitud de onda corresponde al espectro
visible
(400-700 nm) el periodo de vibración es del orden de (asociado a la propagación de la energía
de la onda) coinciden. Si la longitud de onda corresponde al espectro
visible
(400-700 nm) el periodo de vibración es del orden de 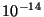 s. Cuando colocamos un detector
(célula fotoeléctrica, cámara de vídeo, ojo)
ante una onda electromagnética, éste no es capaz de seguir
las oscilaciones y por lo tanto detecta un promedio temporal de la
señal.
Así, definimos la intensidad del campo eléctrico como
la media temporal del vector de Poynting. s. Cuando colocamos un detector
(célula fotoeléctrica, cámara de vídeo, ojo)
ante una onda electromagnética, éste no es capaz de seguir
las oscilaciones y por lo tanto detecta un promedio temporal de la
señal.
Así, definimos la intensidad del campo eléctrico como
la media temporal del vector de Poynting.
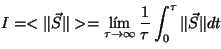 . . |
(2.22) |
Resolviendo la integral anterior, la intensidad detectada, para ondas
planas
es
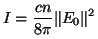 , , |
(2.23) |
mientras que para ondas esféricas tenemos
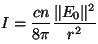 , , |
(2.24) |
resultado conocido como la ley del cuadrado de la distancia.
|

